$$
\begin{align}
{n \choose k} &= \frac{n!}{k!(n-k)!} \quad for \ 0 \leq k \leq n&. \\
{n \choose k} &=
\begin{cases}
{n-1 \choose k-1} + {n-1 \choose k} &\text{0 < $k$ < $n$} \\
1 & \text{$k$=0 or $k$=$n$}
\end{cases}
\end{align}
$$
Binomial Coefficient Pseudocode using Divide-and-Conquer
int bincoeff(int n, int k) |
이항계수를 분할정복법으로 구현하기는 간단하지만 효율적이지는 않다. bincoeff(n-1, k-1)과 bincoeff(n-1, k)는 모두 bincoeff(n-2, k-1)의 결과가 필요하고 이 값은 해당 알고리즘에서 중복 계산되므로 알고리즘의 효율이 떨어진다. 분할정복법은 나눠진 문제들 간에 서로 연관성이 없는 문제를 해결하는데 적합함을 상기하자.
Binomial Coefficient Using Dynamic Programming
Algorithm Design
- Establish a recursive property. B[i][j] will contain $ _iC_j$
$$
B[i][j] =
\begin{cases}
B[i-1][j-1] + B[i-1][j], & \text{0 < $j$ < $i$} \\
1, & \text{$j$ = 0 or $j$ = $i$}.
\end{cases}
$$
- Solve an instance of the problem in a bottom-up fashion by computing the rows in B in sequence starting with the first row.
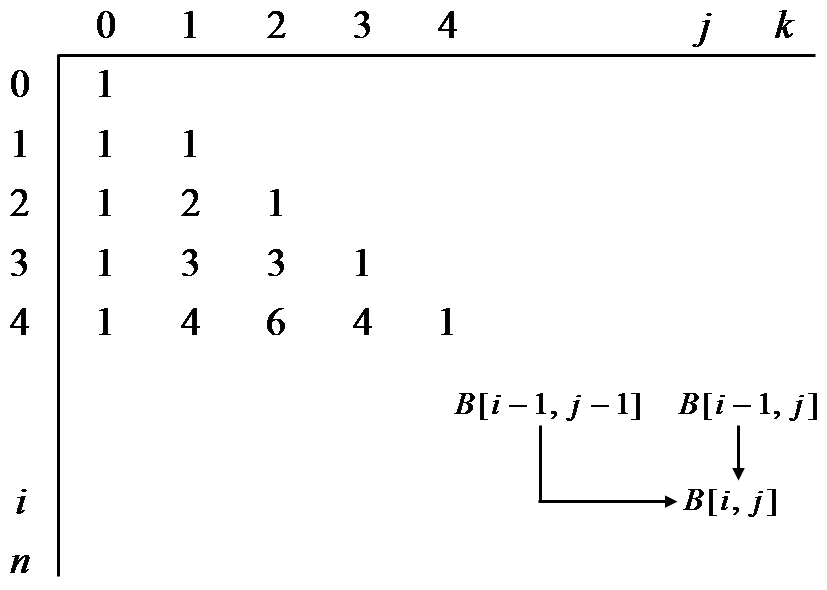
$ _nC_k$를 구하기 위해 B[0][0]부터 시작해서 위에서 아래로 재귀관계식을 적용해 배월을 채워나간다. 결국 최종해는 B[n][k]에 저장된다.
Compute row 0:B[0][0] = 1
Compute row 1:B[1][0] = 1
B[1][1] = 1
Compute row 2:B[2][0] = 1
B[2][1] = B[1][0] + B[1][1] = 1 + 1 = 2
B[2][2] = 1
Compute row 3:B[3][0] = 1
B[3][1] = B[2][0] + B[2][1] = 1 + 2 = 3
B[3][2] = B[2][1] + B[2][2] = 2 + 1 = 3
B[3][3] = 1
Compute row 4:B[4][0] = 1
B[4][1] = B[3][0] + B[3][1] = 1 + 3 = 4
B[4][2] = B[3][1] + B[3][2] = 3 + 3 = 6
Pseudo Code
int bincoeff2(int n, int k) |
Source Code
// File: binomial2.h |
// File: binomial2.cpp |
// File: bincoefftest.cpp |
Time Complexity Analysis
Basic operation
- the number of passes through the for-j loop
Input size
- n, k
Every-Case Time Complexity
- $T(n) = \frac{k(k+1)}{2} + (n-k+1)(k+1) = \frac{(2n-k+2)(k+1)}{2} \in \Theta (nk)$
| i | 0 | 1 | 2 | 3 | … | k-1 | k | k+1 | … | n |
|---|---|---|---|---|---|---|---|---|---|---|
| j-loop 수행횟수 |
1 | 2 | 3 | 4 | … | k | k+1 | k+1 | … | k+1 |
$$
1+2+3+4+ \cdots + k + \underbrace{(k+1) + (k+1) + \cdots + (k+1)}_{\text{$n$ - $k$ + 1 times}}
$$
알고리즘의 성능을 향상시키고 싶다면 위의 소스코드 중 주석 처리한 부분을 참고하면 된다.